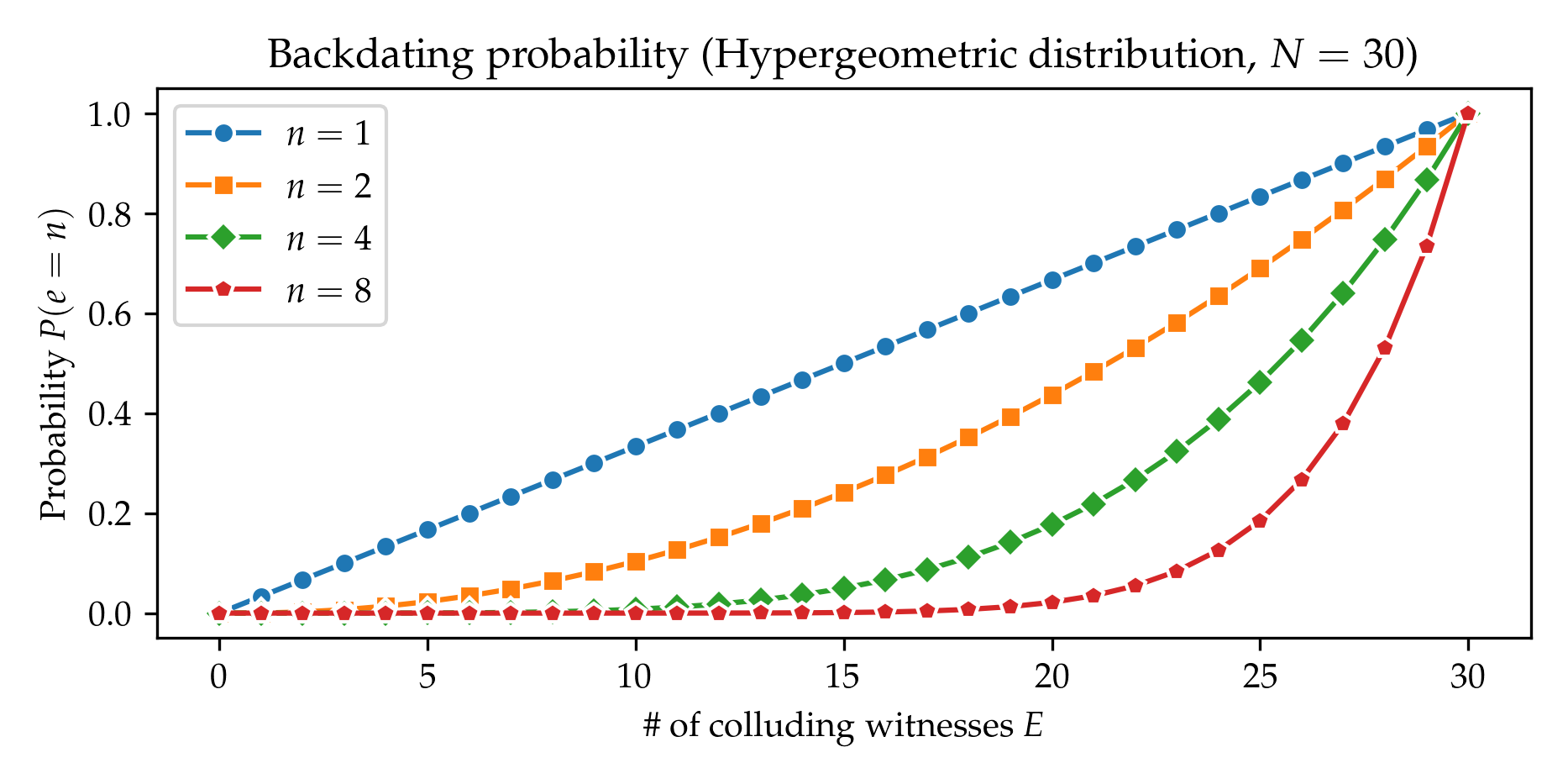
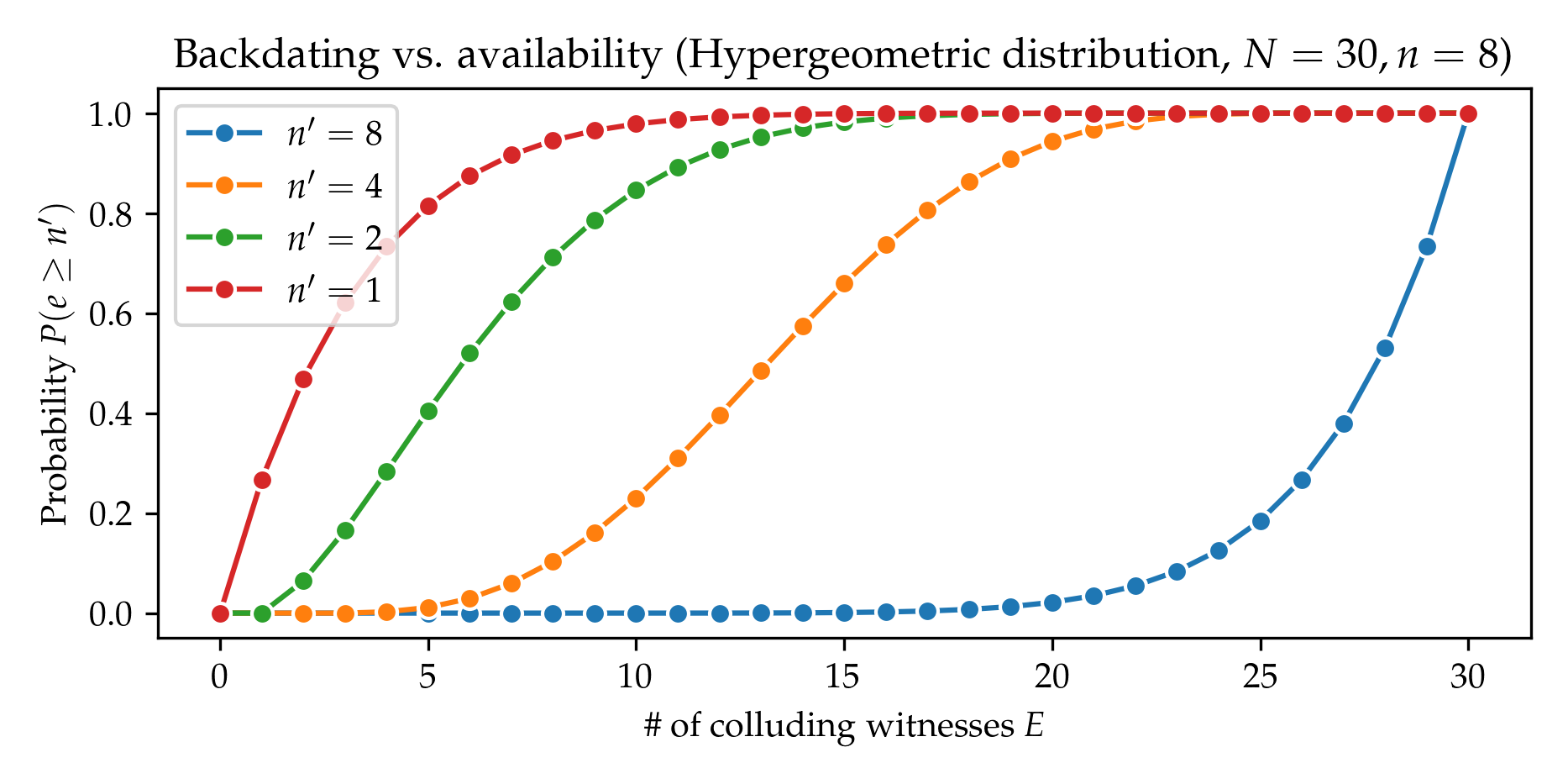
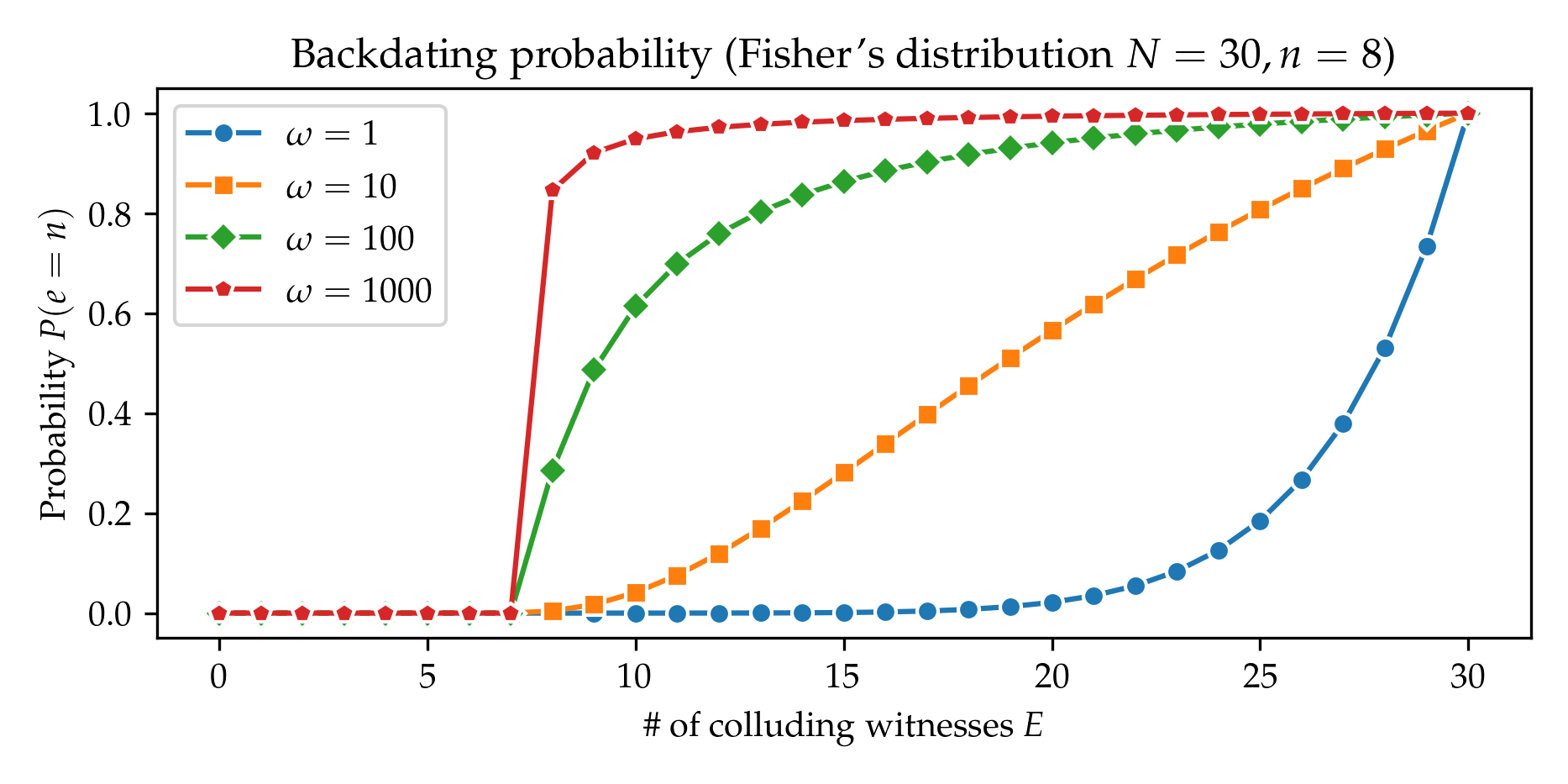
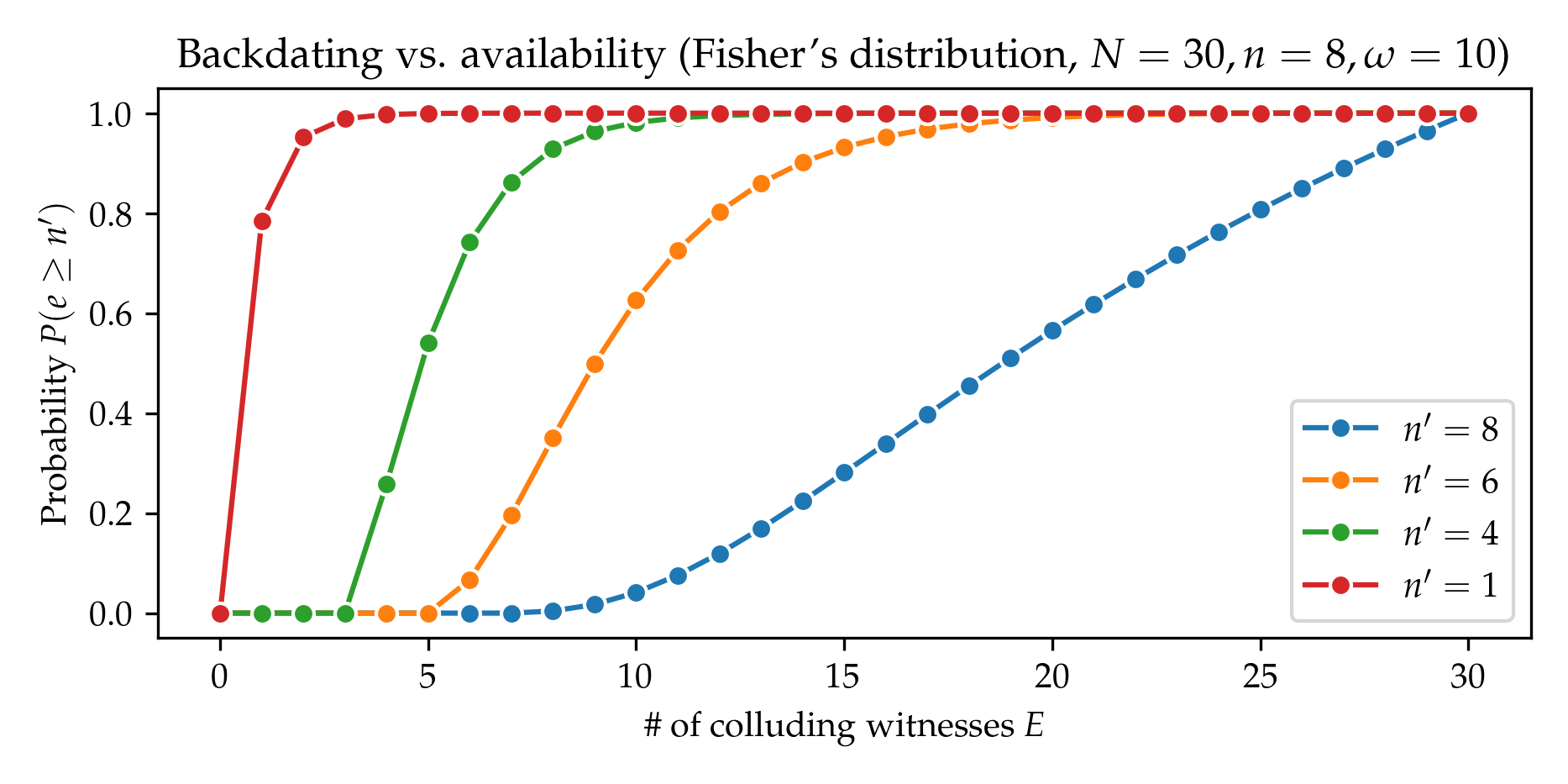
Add figures for probability distributions
Showing
- Makefile 8 additions, 3 deletionsMakefile
- bibliography/bibliography.bib 41 additions, 0 deletionsbibliography/bibliography.bib
- chapters/01_introduction.tex 90 additions, 10 deletionschapters/01_introduction.tex
- figures/backdating_probability_hypergeometric.png 0 additions, 0 deletionsfigures/backdating_probability_hypergeometric.png
- figures/backdating_probability_hypergeometric_available.png 0 additions, 0 deletionsfigures/backdating_probability_hypergeometric_available.png
- figures/backdating_probability_noncentral.png 0 additions, 0 deletionsfigures/backdating_probability_noncentral.png
- figures/backdating_probability_noncentral_available.png 0 additions, 0 deletionsfigures/backdating_probability_noncentral_available.png
- figures/generate_figures.py 66 additions, 0 deletionsfigures/generate_figures.py
- main.tex 9 additions, 6 deletionsmain.tex
- thesis.pdf 0 additions, 0 deletionsthesis.pdf
117 KiB
129 KiB
107 KiB
122 KiB
figures/generate_figures.py
0 → 100644
No preview for this file type