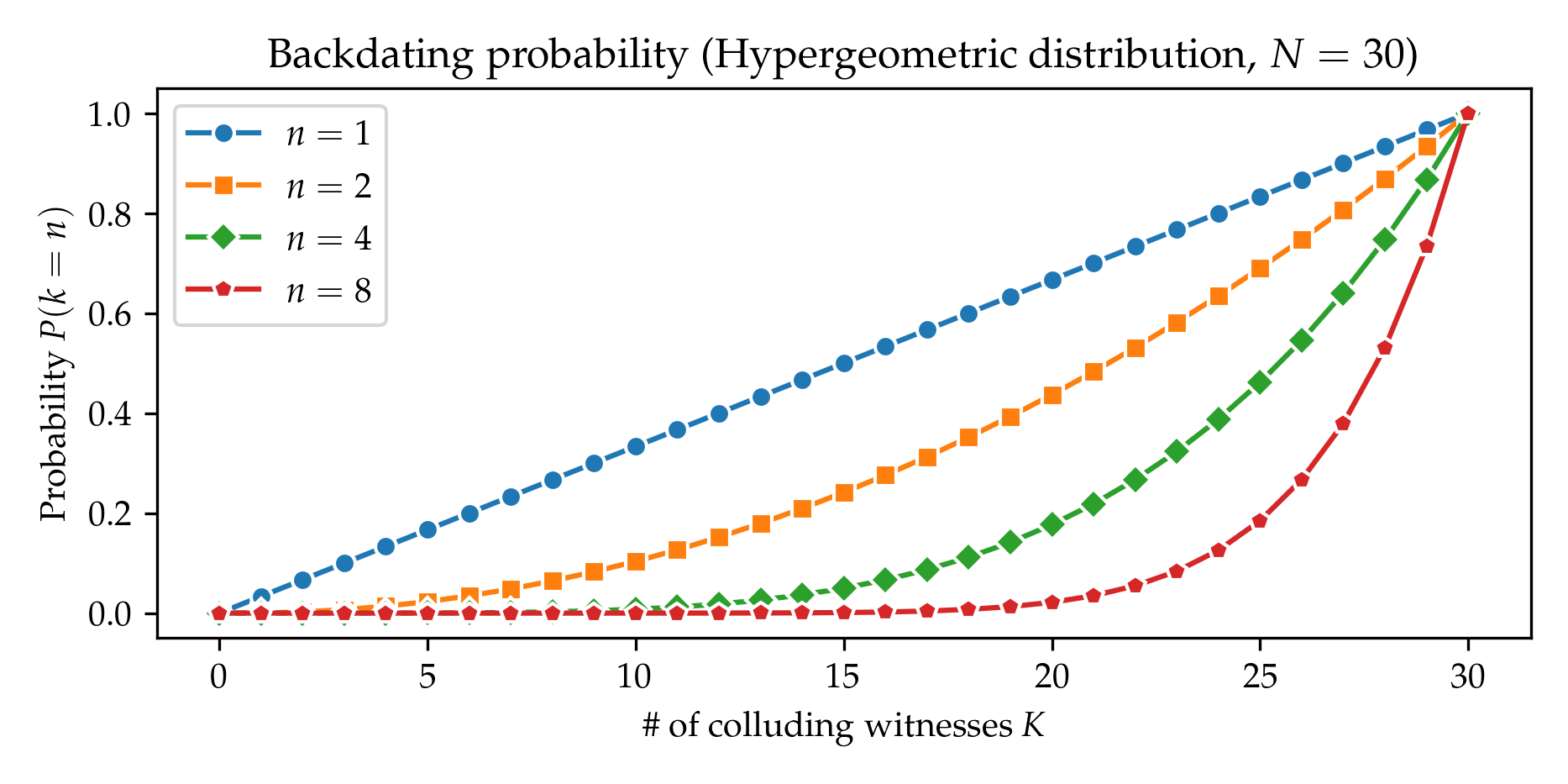
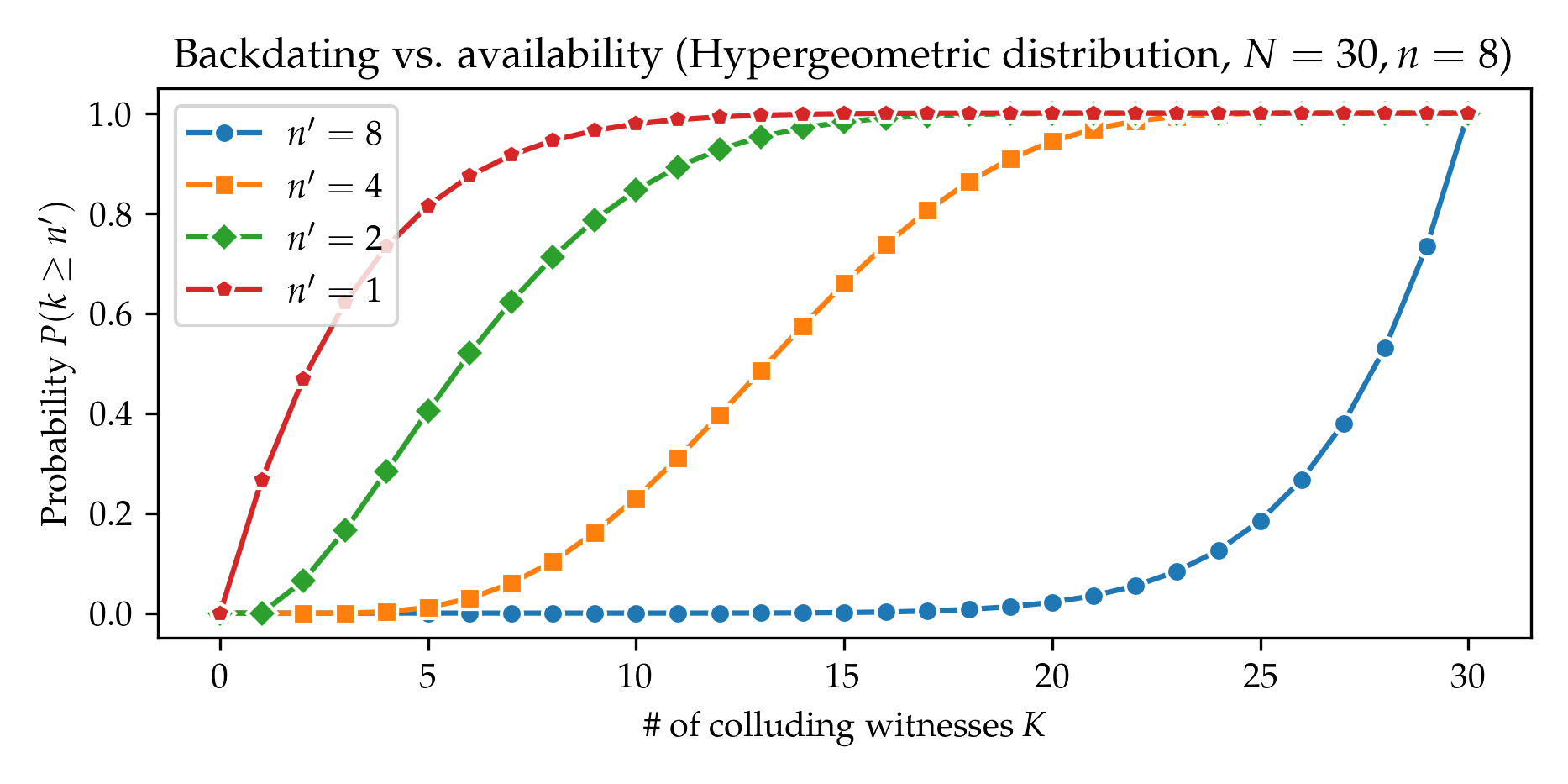
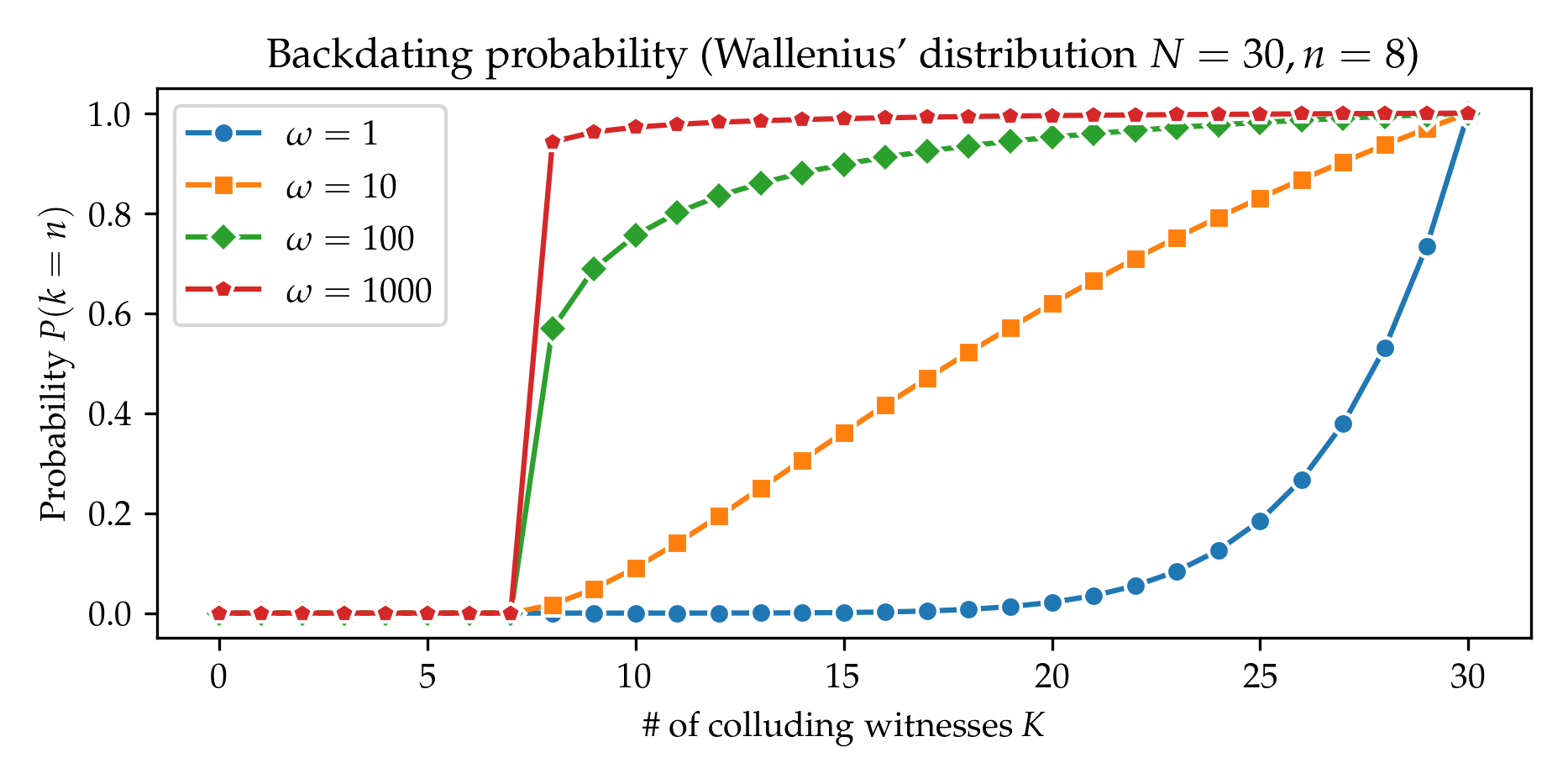
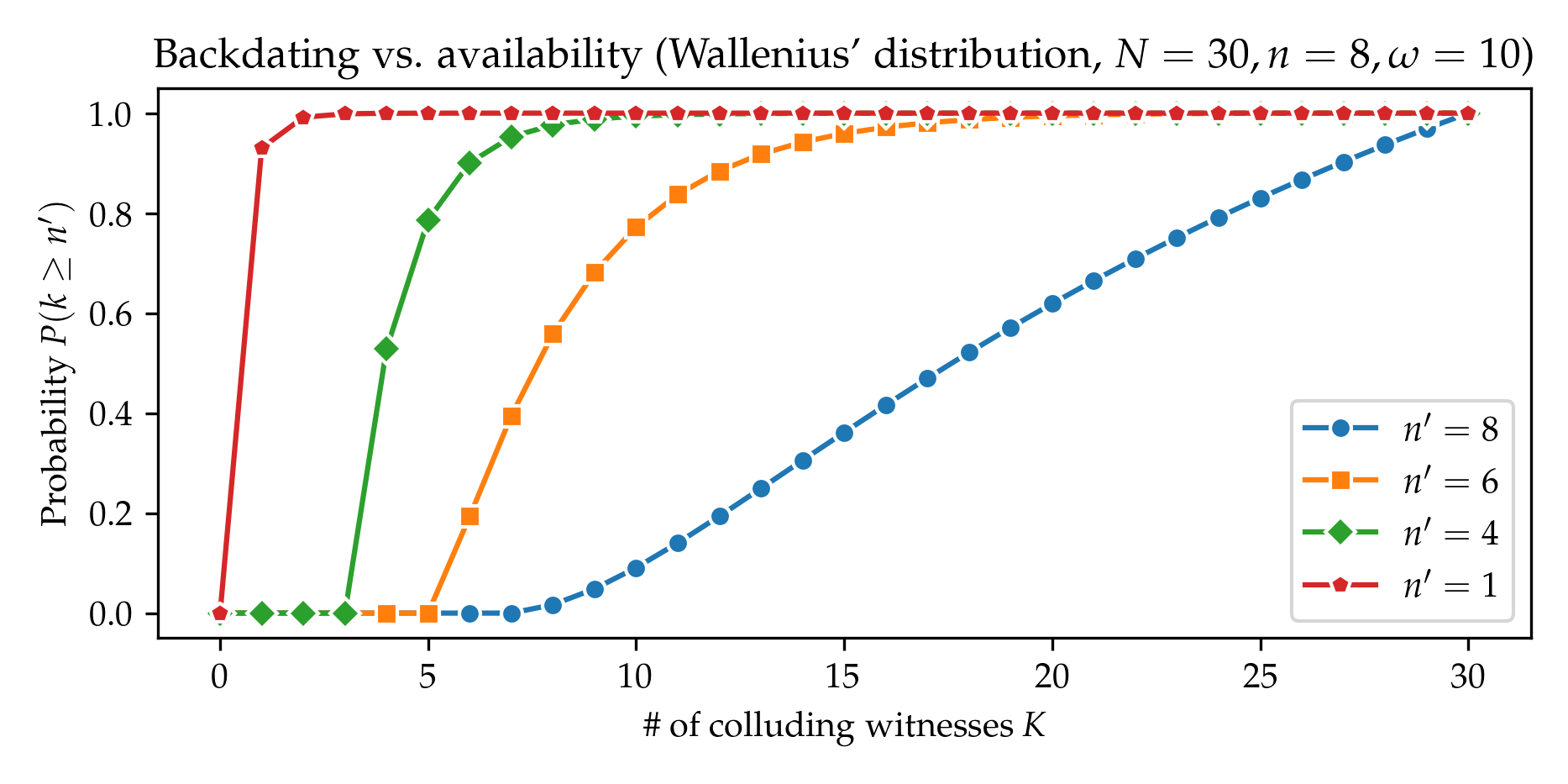
Swith to Wallenius' instead of Fisher's distribution
Showing
- Makefile 3 additions, 0 deletionsMakefile
- bibliography/bibliography.bib 6 additions, 6 deletionsbibliography/bibliography.bib
- chapters/01_introduction.tex 70 additions, 55 deletionschapters/01_introduction.tex
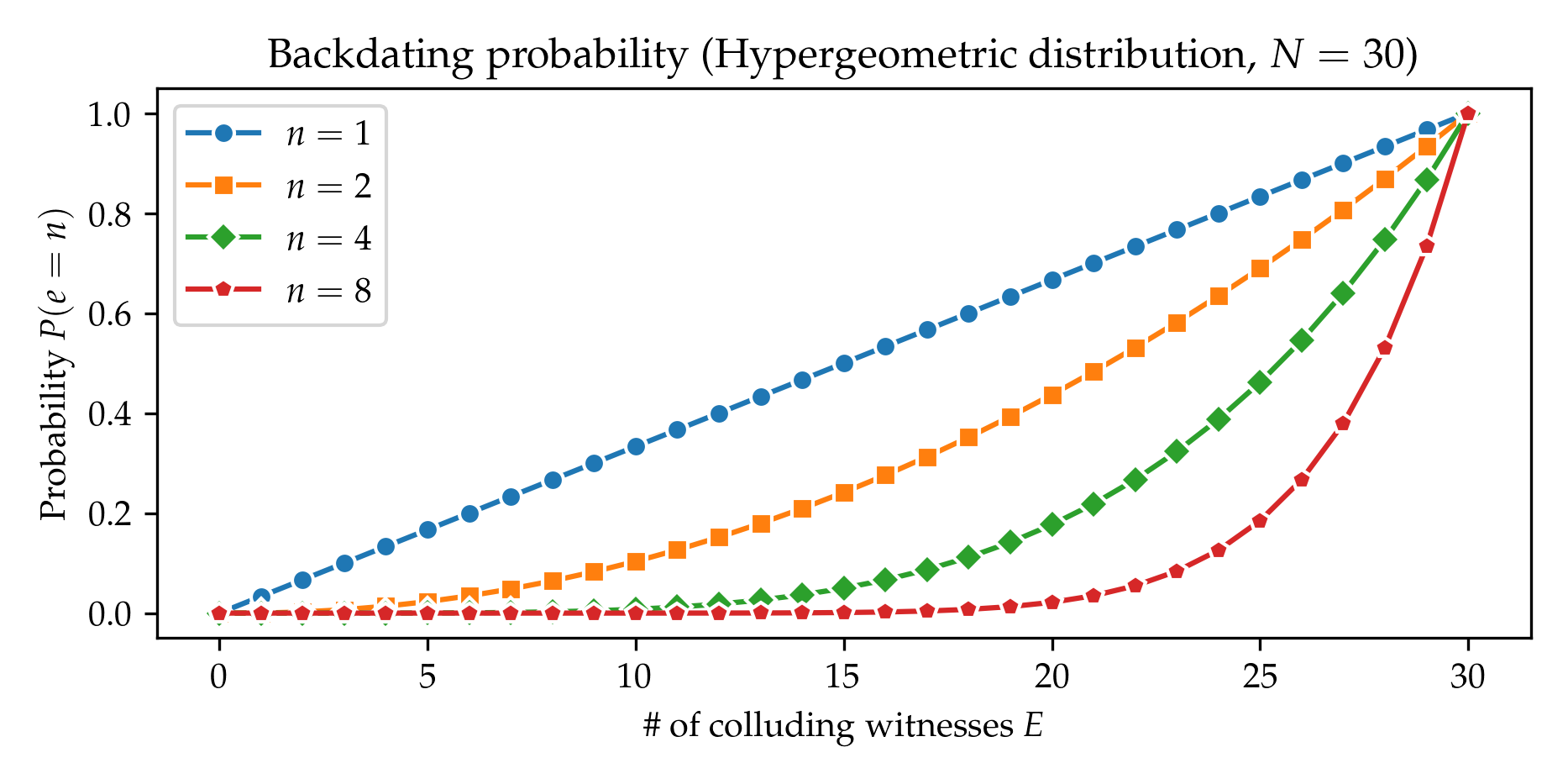
- figures/backdating_probability_hypergeometric.png 0 additions, 0 deletionsfigures/backdating_probability_hypergeometric.png
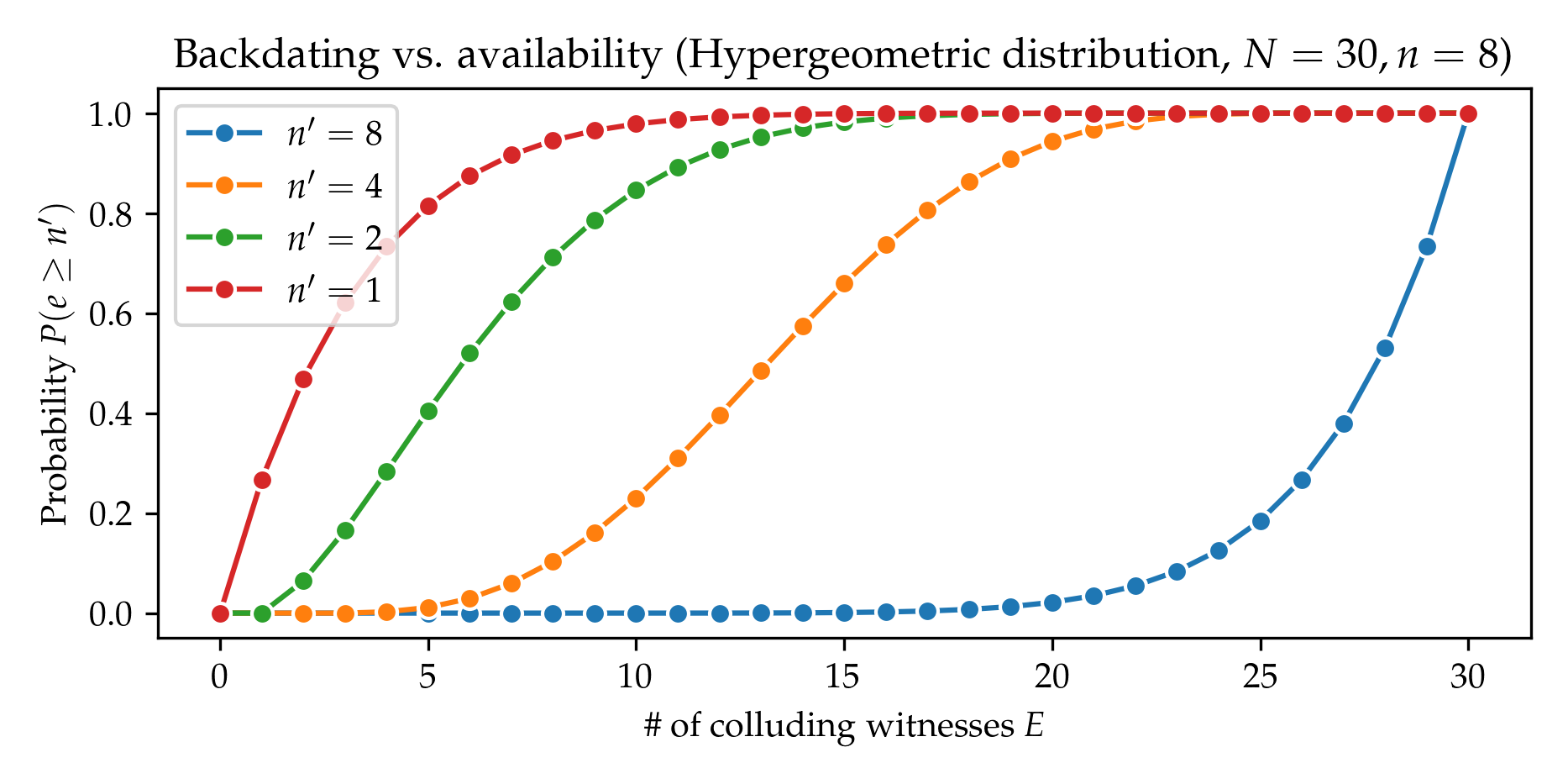
- figures/backdating_probability_hypergeometric_available.png 0 additions, 0 deletionsfigures/backdating_probability_hypergeometric_available.png
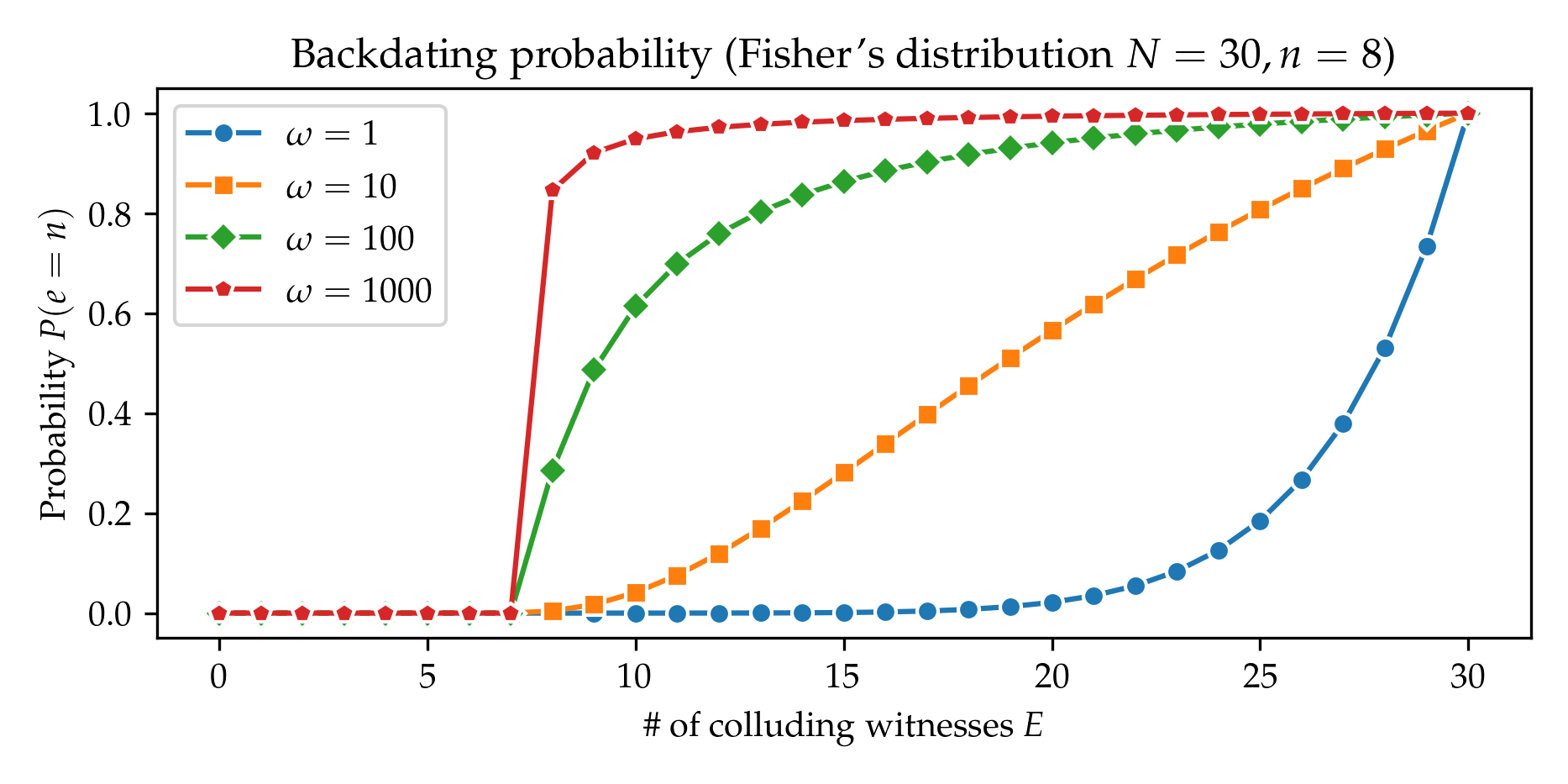
- figures/backdating_probability_noncentral.png 0 additions, 0 deletionsfigures/backdating_probability_noncentral.png
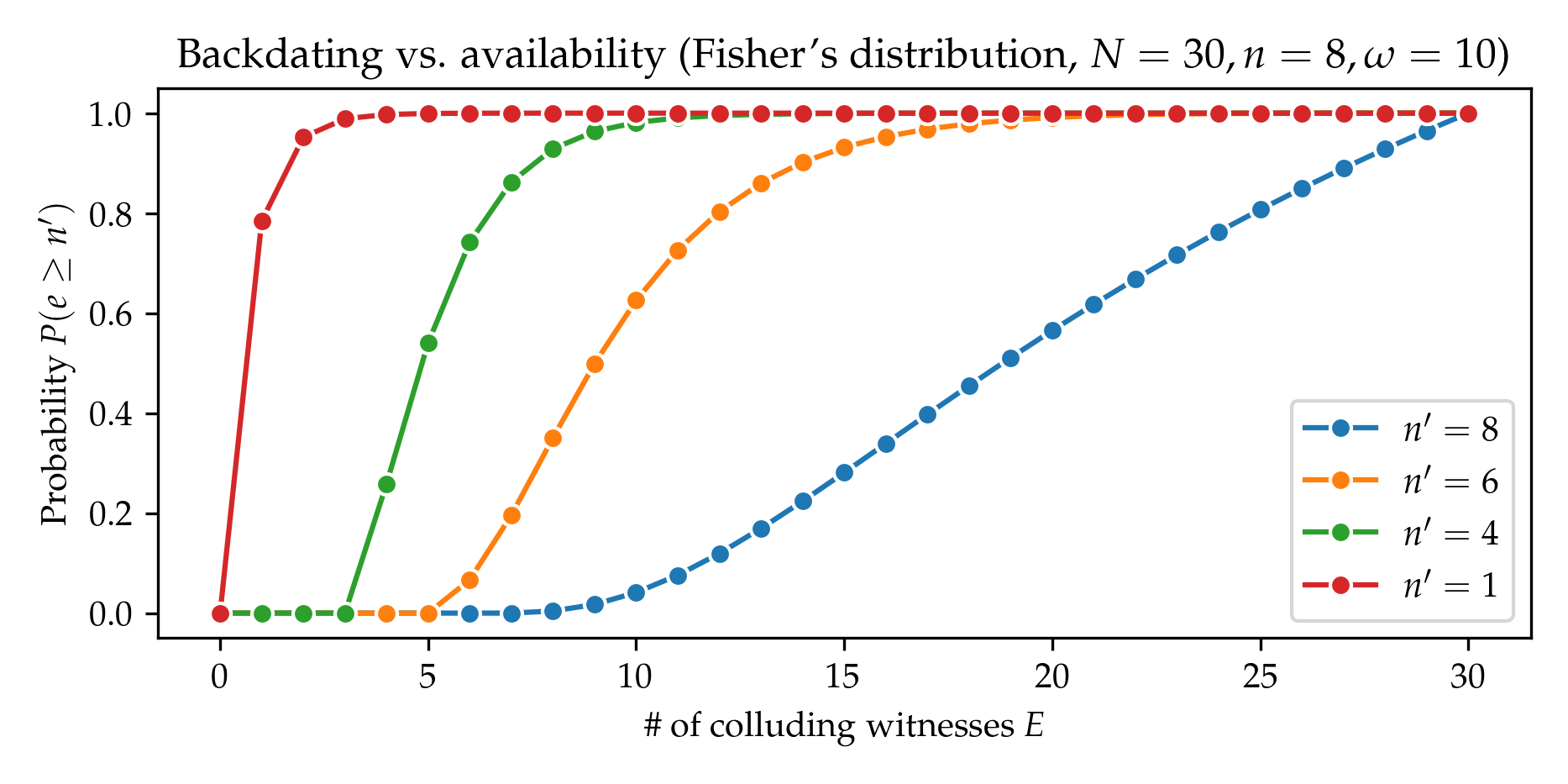
- figures/backdating_probability_noncentral_available.png 0 additions, 0 deletionsfigures/backdating_probability_noncentral_available.png
- figures/generate_figures.py 41 additions, 33 deletionsfigures/generate_figures.py
- main.tex 1 addition, 0 deletionsmain.tex
- thesis.pdf 0 additions, 0 deletionsthesis.pdf
| W: | H:
| W: | H:


| W: | H:
| W: | H:


| W: | H:
| W: | H:


| W: | H:
| W: | H:


No preview for this file type